New information theory-based definitions are not new theories
I'm still working on a synthesis of several threads involving complex systems, cybernetics, machine learning, and economics that Unlearning Economics and I mused about in a YouTube interview last December (he has a new book out BTW). However two things came up that seems to market themselves as such a synthesis, but are in fact ... definitions. One good. One bad.
The good definition
I am conflicted about Erik Hoel. There is work that he is a part of I've found insightful and novel. I've referenced it on multiple occasions (e.g. here, here). In addition to doing neuroscience and mathematical modeling, he is also an author. He is on the side of good on AI art. I feel a kinship in the sense that we both seem to be working on the same general theme of emergence in complex systems (even a bit of neuroscience). But he is also at least rationalist-adjacent, over-generalizes Godel's theorems in that facile pop-science way, over-sells his work, and the novel he wrote is most charitably described as "so bad it's good". Some of these things are my own personal fears or insecurities so there's probably some amount of projection of things I don't like about myself going on.
Anyway. He introduced his new definition on his blog with typical bluster. Now published: My new theory of emergence! exclaims the title. The post opens: "The coolest thing about science is that sometimes, for a brief period, you know something deep about how the world works that no one else does. The last few months have been like that for me." I mean I can relate! That was how I felt about my labor market forecasts. The key, however, is that was comparing theory to data. Hoel's preprint is just theory. And it's mostly just a definition. The preprint's title is more modest: quantifying emergent complexity. And it does what is says on the tin. Creating a quantifiable metric for something is useful. That's what Newton did with momentum. Of course, Newton went on to use that definition of momentum to explain almost all of known physics at the time.
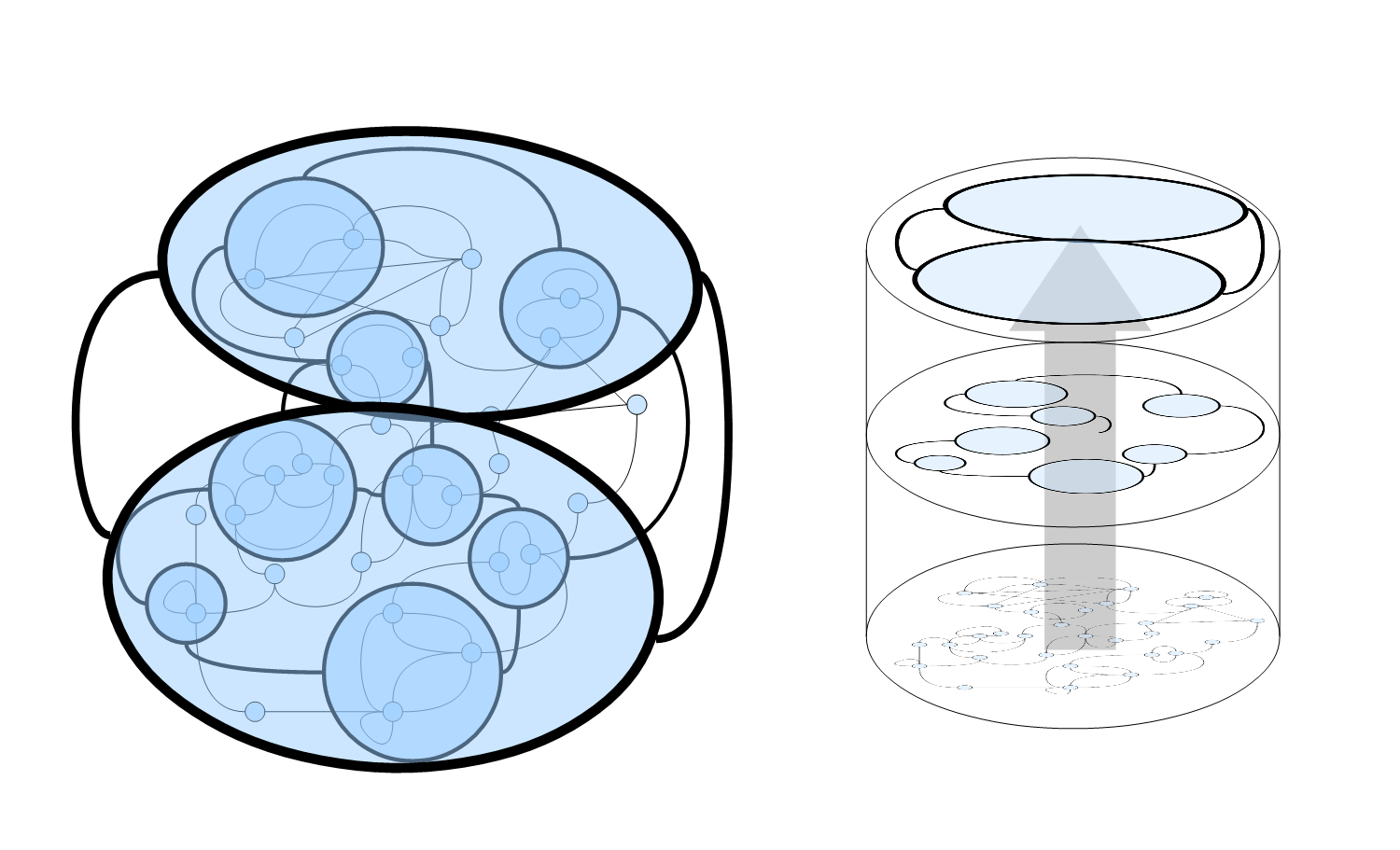
Hoel's definition involves coarse graining at different "scales" from the smallest degrees of freedom all the way up to the entire system as one big holistic element. If you are familiar with electronic circuits, you could see this as combining components–resistors, capacitors, inductors–of a circuit into approximations lumped element models. And then you combine those lumped element models in to larger lumped element models. And so on step by step until the whole system is a "black box" lumped element model. Hoel uses Markov models as his concrete example. Different levels of coarse graining will have different levels of "effective information" (from Hoel's and collaborators previous work [pdf]) based on how well the coarse graining describes the system–how good the approximation is at each step. This latter ingredient, effective information, is where it seems to matter more that we are talking about Markov processes because it's not as well defined outside of that model.
Hoel refers to this coarse graining as creating a higher dimensional object where there may be interactions between the levels of coarse graining. The lower dimension is a specific coarse graining and the "emergent" dimension is the scale of the coarse grainings–the first coarse graining, the second coarse graining, etc up until the coarsest graining in the discrete Markov model example (see the graphic at the top of this post).
What's interesting to me is that this is how emergent dimensions can work in physics. The scaling of one theory at different energies (which relate directly to size) can be sometimes be interpreted instead as a different theory where that energy (size) scale is an emergent dimension. A 4D CFT with energy scaling becomes a 5D supergravity theory. Or a 2D cosmological horizon becomes 4D space time.
While the end-state appears to be well-defined, I am not sure the coarse grainings are unique or even invariant. I'm still working through it, but it's possible you could coarse grain a Markov process using one method and end up with an entirely different set of different emergent scales for the same system. That may be a feature, not a bug. There could well be two different but equally useful dual descriptions of the same system at the same scale.
Regardless, this is still a definition and we don't have any specific examples of where this definition is useful. There are just a couple of examples of how to apply the definition to toy Markov processes and some handwaving. It could be useful! It could actually be the measurand that leads to understanding of emergence! We don't know, but that doesn't make it a bad definition.
The bad definition
Quanta magazine is funny. It was originally where I read the over-selling of Hoel's work on effective information. Several days ago they put out an article over-selling functional information. I do appreciate it when some billionaire turns philanthropist and promotes scientific work for a general audience with a high quality publication. The articles are all well-written and the subjects are sometimes extremely esoteric (e.g. here)–a surprise they'd be written about at all! I guess that's billionaire money for you. It's a better use of it than reinventing the subway but worse.
The functional information paper by Wong et al that Quanta wrote about is, in a word, mathiness. This is an actual line:
M(Ex) equals the number of different RNA configurations with degree of function ≥ Ex
The form of this component of an example of their definition of functional information is basically stolen from thermodynamics where M(Ex) is the analog of the phase volume function and Ex is the analog of energy. And while it's true we could never enumerate every single possible phase space state in a gas with a specific energy since there are ~10²³ particles in a macroscopic system there are several simplifications that allow you to do the relevant integrations and energy is a well defined concept.
Since every RNA configuration, even restricting to configurations of the same length, can in principle yield a protein with a different "degree of function" Ex –and that "degree of function" is itself not well defined – what we know about M(Ex) is precisely nothing. There are no "short cuts": no identical particles, no conservation of energy, no symmetry. You have to know every the product of every RNA sequence and how it works. And some of those proteins don't have explicit uses themselves but only in conjunction with others, so you'd actually have to know every single protein-protein interaction. Basically, it's a definition that's is no better than no definition.
Those "short cuts" are what make parameterizing our ignorance useful in the case of entropy in thermodynamics. The existence of "short cuts" would actually undermine the approach! Assuming all RNA of a certain length encodes for generic degrees of function is antithetical to the aim of understanding the evolution of complexity. No "short cuts" in the functional information parametrization of our ignorance means no usefulness.
Making a good definition bad
Hoel largely restricted himself to Markov processes as concrete examples in his preprint, but hints at his definition being a stepping stone to understanding the emergence of consciousness in his blog (consciousness gets just a cursory reference in the preprint). And while I am generally a fan of wild speculation, this is where we get into Wong et al territory. We'd be talking about coarse graining a neural network at different scales where the inputs and outputs are the result of neurons firing at one scale and the decisions of human beings at another. What even is effective information at that latter scale? How do we measure it?
Now you may think I'm being hypocritical. In my own post about polycrisis, am I not "coarse graining" human beings to the scale of civilization and using information theory to try to gain insights? Basically, yes. However. First, I am actually using it to say the concept of polycrisis, a concept with an independent existence in political science, isn't necessarily unsound. It's like using temperature as an example of an emergent quantity at the macro (coarse grained) scale that has no meaning at the micro scale. Things could easily be like this; here's an example.
Second, and more importantly, those "short cuts" are back. Information equilibrium as applied to macroeconomics makes an assumption that humans are so complex they are effectively random agents. I've called it "inscrutable rationality". This simplifies the problem so that the decisions of human beings no longer matter, but rather the space of the constraints in which they occur does. Of course, short cuts are only as good as their results–the performance of the macro models built with the information equilibrium framework that takes this short cut (among others) is empirical evidence in its favor.
There may yet be "short cuts" we discover in understanding the systems where Hoel's coarse graining of effective information is a useful tool. Maybe the recent explosion of research into machine learning will help find them! But if you'll allow me another prima facie hypocrisy, I can't help but think of this picture:
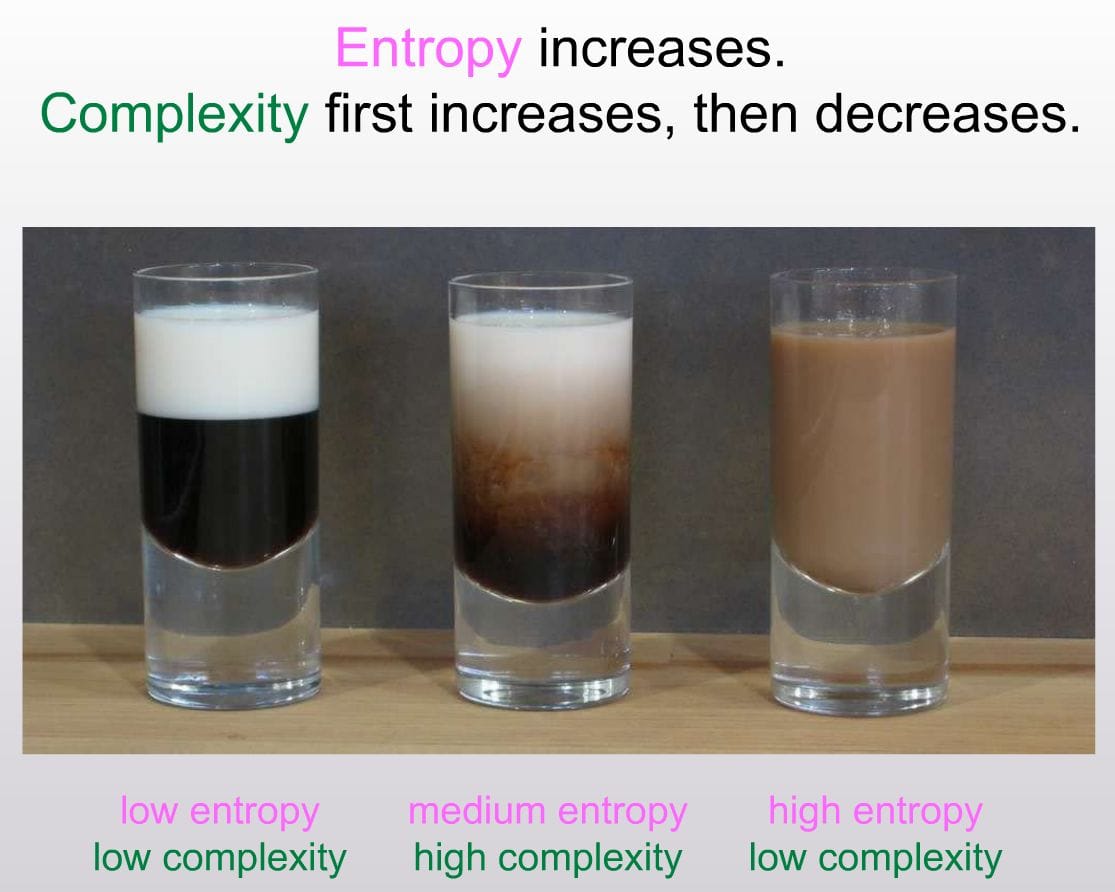
Though that picture is temporal, we could imagine time as Hoel's emergent coarse graining dimension. At the bottom we have particles. At the top we have the basically empty universe with an energy density. We have the emergence of thermodynamics as we move up from the bottom, and the simplification of humanity as inscrutably rational as we head towards averaging over the Hubble volume (let's call it psychohistory for fun). But in the middle, at the peak of complexity, we have a mess. Is that where consciousness resides? No good simplifications? Here (in our heads) be dragons?
I don't know the answer, but I do know that in physics the coarse graining procedure Hoel describes, manifesting as e.g. Wilson renormalization, has an easy theory at one end (protons and neutrons) and an easy theory at the other end (free quarks) ... and a mess in the middle. I know it well! It was what my doctoral thesis was about. I had an effective (coarse grained) description in terms of instanton-mediated 't Hooft vertices and chiral perturbation theory as a step in between quarks and protons–with a degree of empirical success. So I'm not completely averse to some kind of coarse grained description with high effective information per Hoel's theory in between atoms and galaxies. But consciousness could be a mess. It feels like it sometimes.